为何要折半查找:随缘还是投机?
一位同学参加某IT企业校招,编程测试考了一道二分查找(折半查找)题,准备充分的他顺利实现了。面试时考官又问到“为什么我们都用二分查找,而不是三分、四分?”,结果该同学答非所问,讲了一遍二分查找相比顺序查找的优势。所幸其它问题回答尚好,没有杯具。
回顾我们大学课堂中的数据结构/算法课程,往往总是把算法过程一教了事。不怎么勤奋的同学往往觉得过程枯燥,学不过来;勤奋的同学往往也只是强行记下,无法深刻理解算法背后的思想和原理。二分查找本身过程不复杂,就是要在一个长度为\(n\)有序数组\(A\)中找一个数\(x\),我们首先去看数组中间那个数\(A[(n-1)/2]\)是不是\(x\),是的话就查找成功;不是的话,如果中间数比\(x\)大,则到左半个数组中继续查找;如果中间数比\(x\)小,则到右半个数组中继续查找。只要还未找到,就继续这样“折半”下去,折到不能再折时则查找失败。
例子
下图演示了在一个长度为16的数组中折半查找元素\(9\)的过程。初始的查找范围是\(A[0]~A[15]\),则比较\(A[7]\)和\(9\);结果\(A[7]=15\)比\(9\)大,则到左半个数组\(A[0]~A[6]\)之间查找,比较\(A[3]\)和9;结果\(A[3]=8\)比\(9\)小,则到剩下右半个数组\(A[4]~A[6]\)之间查找……依此类推,经过4次比较后,范围已经不能再缩小,判断查找失败。
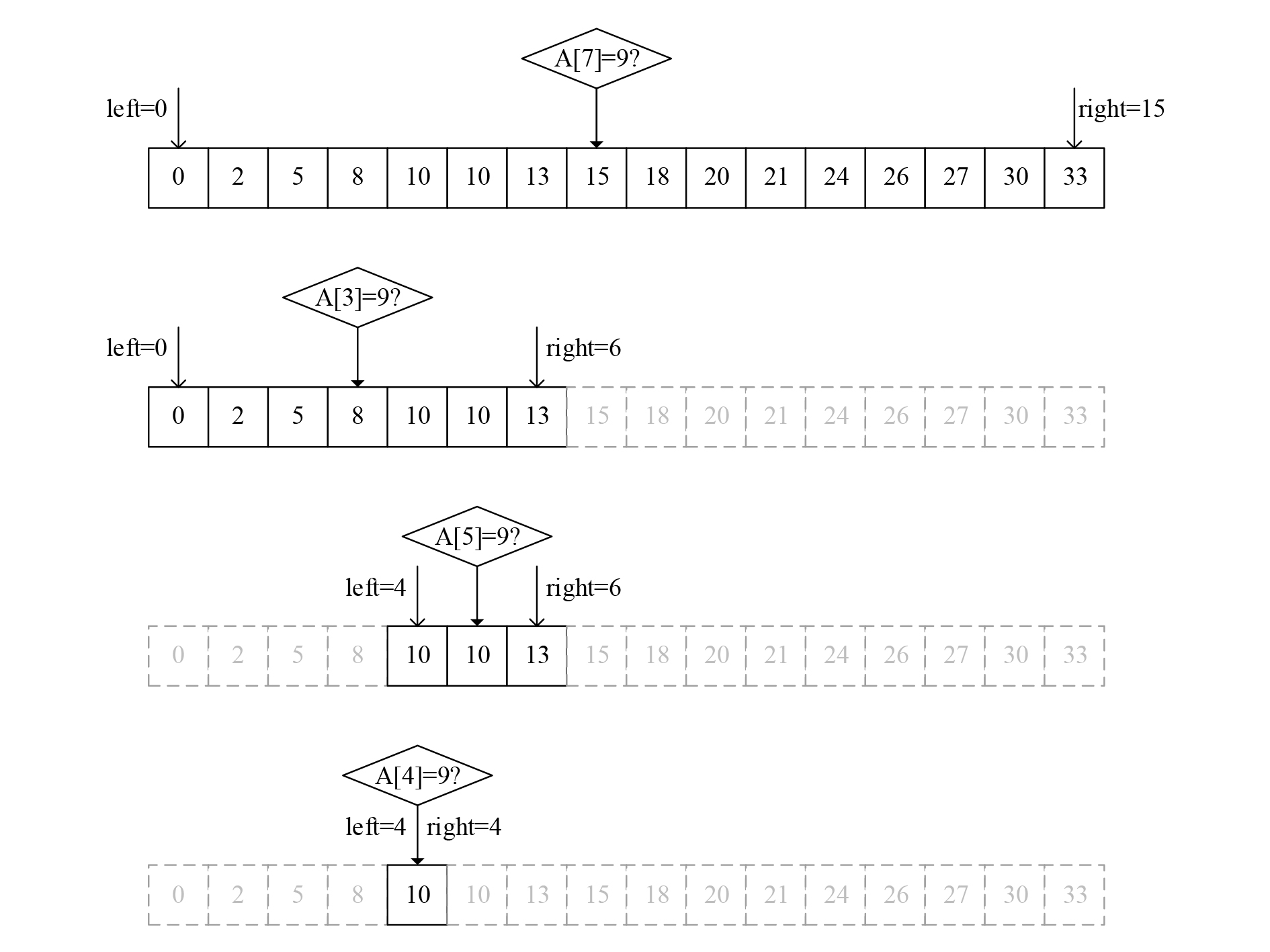
图1 二分查找示例
代码
int BiSearch(int [], int x)
{
int pos = -1, left = 0, right = n - 1, mid;
while (left <= right) {
mid = left + (right - left) / 2;
if (a[mid] == x) {
pos = mid;
break;
}
else if (a[mid] < x)
left = mid + 1;
else
right = mid - 1;
};
return pos;
}
三分怎么样
回到“为什么要二分”这个问题,那就是为什么一开始要拿数组的中间元素和x比较呢?我想“三分”,先拿数组三分之一处的元素A[(n-1)/3]和x比较可不可以?例如对于上面这个数组,最大数是33,我总觉得9更可能在比较靠前的位置啊!回答当然是可以的。下图演示了在该数组中进行三分查找的过程,我们看到要经过5次比较才能判断出数组A中不含元素9。
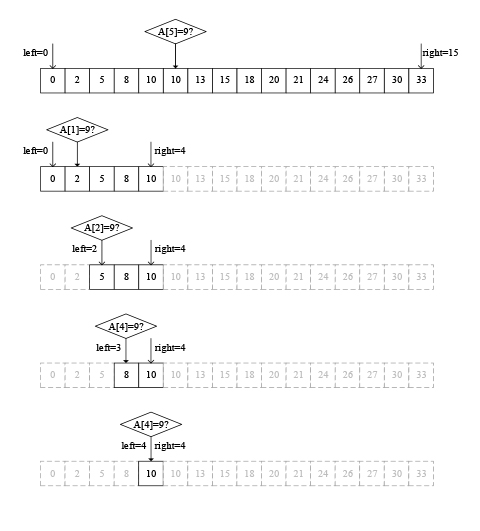
图2 三分查找示例
要实现三分查找的代码,只要把上面程序“\(mid = left + (right-left) / 2\);”这条语句中的2改成3就可以了。
那三分查找一定比二分查找慢吗?当然不一定。假如你要查找的元素正好就在1/3处,那我不就幸运地一步查找成功了?
我们通过程序来比较二分查找和三分查找的平均效率。这里我们随机生成长度为10000的数组,在里面随机查找一个元素,而后执行二分查找和三分查找各100次。结果显示,二分查找平均搜索次数在12.7左右,而三分查找平均搜索次数在13.5左右。
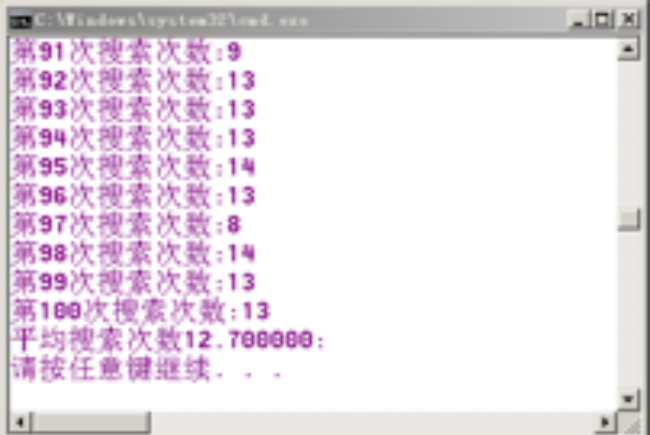
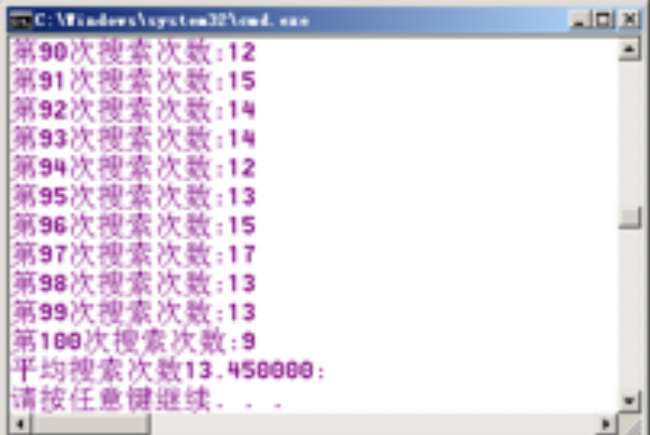
图3 二分和三分查找平均比较次数测试结果
这到底是为什么呢?不是说好的随机生成和查找,凭什么你每次猜中间就会快一点,我猜三分之一处就会慢一点?是不是只有每次猜中间是最快的,猜其它地方都会变慢?
基于概率的解释
其实关键不在于“每次猜哪个位置更可能猜中?”,而是在于“如果这次没猜中,我能够得到多少信息?”如果我每次猜中间,其实我默认在查找前不掌握任何信息,那么搜索的数x有一半概率在数组前半部分、有一半概率在数组后半部分;比较完数组中间数和x之后,下次我就能将查找范围缩小一半——至于是前半部分还是后半部分,随缘就好。
如果你每次猜三分之一,其实你心理倾向于x在数组前三分之一部分的可能性更大:如果A[(n-1)/3]比x大,那么恭喜你,一次性就将查找范围缩小到1/3,这就优于二分查找;反之,很遗憾,你这次只将查找范围缩小到2/3,这就劣于二分查找。这种做法是带有投机性的,那么投机成功的可能性有多大?我们可以做个计算,在没有任何先验信息的条件下,x在数组前1/3部分和后2/3部分的概率分别是1/3和2/3,那么每次猜三分之一处,通过比较,查找范围将期望缩小到原来的:
$$\frac{1}{3} \times \frac{1}{3} + \frac{2}{3} \times \frac{2}{3} = \frac{5}{9}$$答案就出来了,执行二分查找,每次猜测比较后范围能缩小到一半;执行三分查找,每次猜测比较后范围平均缩小到0.5555\(\ldots\)所以三分查找的平均比较次数是二分查找的1.1111\(\ldots\)倍。
更一般的,如果每次猜数组第p处的元素(p可以是1/2、1/3、1/4、0.618等等),那么每次比较后查找范围将期望缩小到:
$$p^{2} + (1-p)^{2}$$可知当p=1/2时,上式有最小值0.5,所以二分查找优于其它各种p分查找。
对最坏时间复杂度进行分析,我们知道二分查找的复杂度是\(O(\log_2n)\),这也是各种p分查找中最低的;如三分查找的复杂度会是\(O(\log_{1.8}n)\)。
综上所述,如果你遇上考官问你“为什么我们都用二分查找,而不是三分、四分?”,正确的回答是“采用二分查找,每次比较后,查找范围将缩小到原来的1/2;而采用其它位置查找,每次比较后,查找范围缩小的期望值都大于1/2”。
觉得这个解释不够高大上?行,下面介绍一个更能彰显你才华的回答,从气势上压倒考官。
基于信息熵的解释
这个回答是这样的:“查找前不确定性最大,即信息熵最大;根据信息熵原理,二分查找能够使得每一步得到的期望信息增益最大,从而尽快减少不确定性”。
信息熵的概念来源于热力学第二定律,信息论之父香农(Shannon)给出的定义如下:
$$H(X) = -\sum_{x \in X}p(x)\log(p(x))$$其中p(x)表示随机事件x的概率。最大熵原理认为,学习概率模型时,在所有可能的概率模型中,熵最大的模型是最好的模型。
对于查找问题,因为查找前我们什么都不知道,即x位于数组A中每个位置的概率都是1/n,此时我们拥有的信息熵为:
$$H(X) = -\sum_{i=1}^{n}\frac{1}{n}\log(\frac{1}{n}) = \log n$$采用二分查找,每次比较中间位置后,忽略正好找到x的这个小概率事件,则无论判断出x落在左半边还是右半边,信息熵都变为:
$$H_{1}(X) = -\sum_{i=1}^{n/2}\frac{2}{n}\log(\frac{2}{n}) = \log n - \log 2$$期望的信息增益就是:
$$G_{1} = \log n - \frac{1}{2}(\log n - \log 2) - \frac{1}{2}(\log n - \log 2) = 1$$(注:把中间位置正好找到x的概率考虑进去也很简单,只不过公式会变得比较难看)。
采用三分查找,每次比较后,如判断出x落在左三分之一区间,信息熵变为:
$$H_{2}(X) = -\sum_{i=1}^{n/3}\frac{3}{n}\log(\frac{3}{n}) = \log n - \log 3$$如判断出x落在右三分之二区间,信息熵变为:
$$H_{2}(X) = -\sum_{i=1}^{2n/3}\frac{3}{2n}\log(\frac{3}{2n}) = \log n - \log \frac{3}{2}$$期望的信息增益就是:
$$G_{2} = \log n - \frac{1}{3}(\log n - \log 3) - \frac{2}{3}(\log n - \log \frac{3}{2}) \approx 0.918$$也就是说,二分查找的每一步使信息的不确定性减少1,最多经过log n步,信息熵降为0;而三分查找的每一步使信息的不确定性平均减少约0.918,要达到完全确定性,所需的步骤多于二分查找。
简而言之,最大熵原理要求我们(1)满足已知信息;(2)不做任何未知假设。对于查找问题,如果我不掌握任何信息,我就默认x在数组任何位置的概率都是相同的,所以我不做任何投机,就从中间进行猜测和拆分。这里出总结我的一条人生箴言:
不掌握信息,就不做投机。
猜心程序、决策树和信息熵
必应问答是一个智能小程序,它让你心里先想一个名人的名字,而后问你一些有关这个人的问题,比如“这个人是女的吗”,“是演员吗”,“是足球运动员吗”,“是中国人吗”,“得过冠军吗”等等(回答只能是“是”和“否”),最后猜出你心里想的这个人是谁。

分析一下就知道,该程序的设计原理就是维护一个名人数据库,在其中记录每个名人针对上述问题的答案。那么,程序要按什么顺序提问,才能够尽可能快地猜出正确结果?
这个问答过程其实就是个决策过程。刚开始,程序对用户心里想的人是谁一无所知,信息熵最大。为了尽早猜到这个人,程序希望通过问答尽快减少信息熵。不妨假设,在名人数据库中,男的占60%,女的占40%;演员占15%;足球运动员占8%;中国人占20%……为了使信息的期望增益最大,应当先问比例划分最均匀的那个问题。如先问关于名人的性别问题,那么有60%的可能排除40%的名人,还有40%的可能排除60%的名人。如果先问这个人是不是演员,投机性就比较大,回答“是”的话就能排除85%的名人,但有85%的可能只排除15%的名人。
注意程序每一步执行之后,都要重新计算比例划分。如先问性别,回答是“男”,那么下一步要先计算男的名人中,演员占多少、足球运动员占多少、中国人占多少……,然后再选比例划分最均匀的那个问题。依此进行下去,“猜心”所要问的问题数量的期望值是最小的。这在机器学习中称为决策树算法,它依据的也是信息熵原理。
扩展思考与练习
- 如果查找时不做固定拆分,而是每次在查找范围内随机取一个位置进行比较,而后根据比较结果缩小查找范围,那么算法的平均比较次数和最坏时间复杂度是多少?
- 二分查找是基于查找前我们不掌握任何信息的前提。那我们是否可以尝试在比较拆分前去获取和利用一些信息?比如已知数组元素值范围在[0,33]之间,要查找元素9,靠前一点查找真的没有用吗?
- 我们知道数据库可以做多表联合查询,如在学校数据库中查找属于计算机专业、数据结构成绩不低于80分、企业实习时间不少于30天的同学,查询语句可以写成:
SELECT Student.name FROM Student, Score, Practice
WHERE Student.id = Score.student_id
AND Student.major = “计算机”
AND Score.course = “数据结构”
AND Score.score >= 80
AND Student.id = Practice.student_id
AND Practice.days >= 30
其中Student, Score, Practice这三张表中分别用于存放学生基本信息、课程考试成绩、学生实习记录。那么数据库在后台执行该查询时,应该先查哪张表、再查哪张表?
参考资料
[1] 《统计学习方法》 李航
[2] 《机器学习》 周志华
[3] 图解最大熵原理, https://blog.csdn.net/yangziluomu/article/details/81986271